Di Fibonacci, matematico pisano, si è detto di tutto e di più. La sua famosa successione 1 – 1 – 2 – 3 – 5 – 8 – 13 – 21…… ormai compare in tutti i thriller e romanzi gialli.
Quindi in questo breve articolo non vi parlerò delle sue similitudini con elementi e fenomeni della natura, ma mostrerò e dimostrerò la sua relazione con la proporzione aurea.
Osservando la successione di Fibonacci si deduce facilmente qual è la regola generatrice dei suoi termini:
Fn = Fn – 1 + Fn – 2
Vediamo dunque di calcolare il valore del limite, al tendere di n a +∞, del rapporto Fn+1/Fn tra un termine della successione e quello precedente (supponiamo che tale limite esista finito…si può dimostrare rigorosamente).
Vogliamo determinare dunque il valore di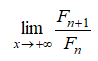 
.
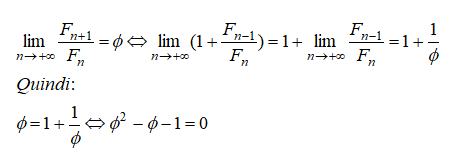
Il limite cercato è dunque la soluzione positiva dell’equazione nell’incognita Ø che è pari a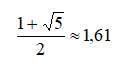 
. Tale limite come si vede coincide con il famoso rapporto aureo o proporzione divina.
Link utili: